Normalizing Flows, a Simple Example

This post is meant as an exercise in implementing a generative normalizing flows model in a 2D environment. The full notebook can be found on github. It will assume some prior knowledge of Jax/Flax and normalizing flows. You also need to know (or be willing to learn) some fundamental concepts in multi-variable calculus, probabilities, etc. I will cite the resources that I found helpful as needed. Personally, I find it's best to set aside a few days for each topic separately, rather than trying to learn multiple things at once.

To familiarize yourself with Jax/Flax, I would recommend this notebook by University of Amsterdam's Deep learning course (which also has other must read resources included). The Jax documentation is also essential. If you are already familiar with numpy and another deep learning library, learning the basics of Jax should take somewhere between a few hours to a couple of days. To get an understanding of normalizing flows (without reading a 50+ page paper) you can take a look at one or more of the following links:

  • Lilian Weng's blog: Good rundown of the theory and many of the common functions.

  • Eric Jang's blog: Theory and a tensor-flow (🤮) implementation. I found the code hard to follow since a lot of magic happens in tensor-flow. Eric has since made a pure Jax tutorial as well, which I highly recommend once you're comfortable with the theory (and if you don't want to bother with flax/optax).

  • UVADLC notebook: Helpful, but much of the content focuses on dealing with the specifics of image data processing and advanced architectures, which can make learning the fundamentals very difficult. I've simplified their code for parts of this tutorial.

  • Normalizing Flows using Pyro library: Pyro tutorials are great in that they focus on conveying a fundamental understanding of the topic rather than the specifics of the library, but I think implementing your own solution in a simplified setting is necessary before using any libraries.

I will briefly go over the basic theory behind normalizing flows as a refresher, and also to establish the variable names that will be used in the code.

Change of Variables

To reiterate the example given by Eric Jang, lets say you have a continuous uniform random variable and its probability density function (PDF) where is a real valued output of . Lets say we applied a function to the outputs of . The result can be treated as a new random variable with its own PDF function . Where is the output of , and . Change of variables theorem helps define .

Let's say we give the range of , we know what the PDF for would look like, since it's uniform.

What would this distribution look like for ? Well, it should be clear that given the range of , would have the range . In this case, it's easy to calculate without change of variables theorem. Intuitively, is uniform and covers the values between 1 and 3. Since the area under the curve should sum up to 1, then the distribution for should look something like the figure below.

But can we prove this mathematically? Yes!

This is an example in 1D, but using change of variables theorem to determine changes in probability distributions is the basis for normalizing flows. The term is really the determinant of the Jacobin of a multi-variable function , which in a 1D environment is equal to the derivative of . If you want to know what a Jacobian is, Khan academy has a few short videos plus a quiz which I recommend (it should take about an hour at most if you already know how to take simple derivatives).

Code for 1D Example:

Defining the problem setting and solution in code might seem trivial if we know the answers already. But I found it a helpful exercise before expanding this idea to a 2 or more dimensional setting.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# let's say we have a valid probability distribution where x is between [0,1] and p(x) = 1 

from scipy.stats import rv_continuous # scipy has a base class for continuous distributions. You do not have to inherit from it.

# function f, and its reverse
def fn(x, reverse = False):
    if reverse:
        return x/2 - 1
    else:
        return 2*x + 1

class x_dist(rv_continuous):
    def _pdf(self, x):
        return np.where((x>0) & (x<1),1,0)
    
px = x_dist()
x = np.linspace(-0.5,1.5,100)
h = plt.fill_between(x,px.pdf(x),color="blue")
plt.legend(handles=[h], labels=["pdf of X"])

1
2
3
4
5
6
7
8
9
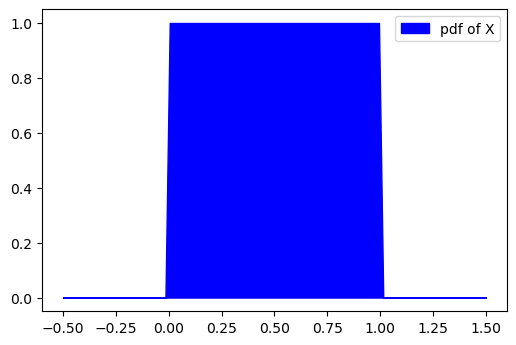
# now we know that if x is being projected by f(x), then px will be projected by 1/2
# f(x) = y
# pydy = pxdx
# py = px (dx/(dy) = px (dx/(d(f(x))) = px/(f') = px/2 = 0.5px
# so Y PDF will look like this: 
y = fn(x)
py = 0.5 * px.pdf(x)
h = plt.fill_between(y,py,color = "g",)
plt.legend(handles=[h], labels=["pdf of Y"])

Normalizing Flows in 2D with Jax

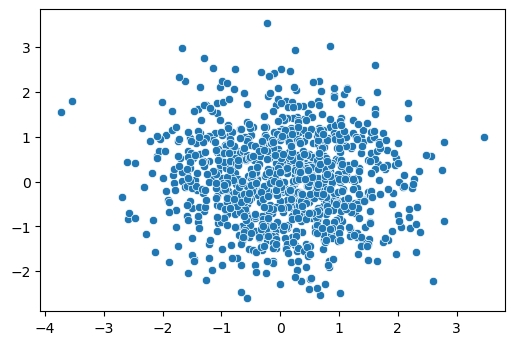
Let's define the same 2D dataset as Eric Jang's problem. We generate 1024 samples, and each sample has 2 points. There is a relationship between the two points; to create a generative model, we want to find a series of invertible functions which can untangle the "complicated" relationships, and project each point to a unimodal normal distribution. If successful, generating new samples is trivial: we take 2 samples from a gaussian distribution and stack them as , and send backwards through the flow. In other words, transform by reversing the order of functions and sending it through the inverse of each function. An implication of this is that dimensionality remains the same in normalizing flows.

1
2
3
4
5
6
7
8
# define a target distribution
def get_points():
    x2 = 0 + 4 * np.random.normal()
    x1 = 0.25 * x2**2 + np.random.normal()
    return x1,x2
x_samples = np.array([get_points() for i in range(1024)])
t_dist = jnp.array(x_samples)
sns.scatterplot(x = x_samples[:,0],y = x_samples[:,1])

Regardless of your target distribution, after going through the flow, you want to final distribution to be a multi-variable normal distribution with no covariance/correlation. We assume the marginal distribution of each point after the transformations to be normal, and calculate the loss based on this assumption. This means that during training, the parameters of the functions are adjusted such that the points are projected into a multi-variate normal distribution, so something like this:

But how do we calculate this loss value? This is a critical step that did not click with me right away. If my explanation isn't clear makes sure to read one of the recommended posts mentioned early on. Let's assume the flow only has 1 function, .

We know that , which can be rewritten by replacing with the determinant of the Jacobian of and taking the log of both sides: We have k (for this example, ) samples of (i.e, inputs are (), and and we want to generate new samples that fit . We can project each to a value using a parameterized function , then calculate the PDF of the two points in under a normal distribution. Now we have , and can calculate the log determinant of the jacobian (LDJ) of the transformation, making it possible to calculate (which you can define as the sum of probabilities for each of the two points) using the formula above. We want to maximize , the probability of the samples, therefore is minimized during training. The parameters of will be adjusted during training to minimize the loss function.

In the next section, we'll write the code for this process :)

Defining Functions

We implement leakyRelu and realNVP, two common functions/layers used in normalizing flows. When defining layers, we have to define how it transforms an input, and also how to calculate the log determinant of the jacobian (LDJ). LDJs are passed through and added up in every layer, and are needed to calculated the projected probabilities. The probabilities are then used to calculate the loss of the network.

Relu

In a LeaklyRelu layer, if an input , it is multiplied by a value , else, it is unchanged. The LDJ for each individual point in a sample is:

Here, is either 1 or 2 since each sample is in 2D. Since the final goal is to calculate the loss function, you can sum up the LDJ values before passing it on to the subsequent layer.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# using Flax's nn module
class LeakyRelu(nn.Module):        
    layer_type = "leaky_relu" # a name that will be used when plotting intermediate layers
    def setup(self):
        self.alpha = self.param('alpha', nn.initializers.uniform(0.9), (1,)) # alpha is randomly sampled from a uniform distribution between 0 and 1
    def __call__(self, z, ldj,rng, reverse=False):
        rng, new_rng = jax.random.split(rng, 2)
        if not reverse:
            dj = jnp.where(z>0, 1, self.alpha)
            z = jnp.where(z>0, z, self.alpha * z)
            ldj += jnp.log(jnp.absolute(dj)).sum(axis=[1])
            return z, ldj, new_rng
        else:
            z = jnp.where(z>0, z, z/self.alpha)
            dj = jnp.where(z>0, 1, 1/self.alpha)
            ldj -= jnp.log(jnp.absolute(dj)).sum(axis=[1]) 
            return z, ldj, new_rng

You can visualize the effect of the layer.

1
2
3
4
5
6
7
8
9
10
11
# initialize an lru layer 
lru = LeakyRelu()
rng, inp_rng, init_rng = jax.random.split(rng, 3)
params = lru.init(init_rng,x_samples,0,inp_rng)

# go forward and check LDJ
z = t_dist
ldj = jnp.zeros(len(z))
sns.scatterplot(x= z[:,0], y = z[:,1],label="original")
z,ldj,rng = lru.apply(params,z,0,rng,reverse=False)
sns.scatterplot(x= z[:,0], y = z[:,1],label="forward")

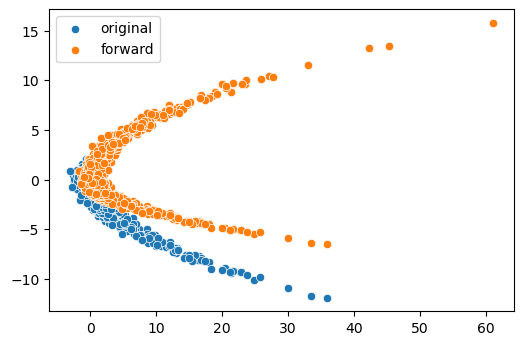Inspecting the the params and LDJ values should look something like this: 

1
2
3
4
5
6
7
FrozenDict({
    params: {
        alpha: DeviceArray([0.73105997], dtype=float32),
    },
})
ldj list: [-0.31325978 -0.31325978  0.         ... -0.31325978 -0.31325978
  0.        ]

where the outputs can take 3 values: 0, , or (if both points were less than 0). Note that .

Coupling Layers

A coupling layer is a layer where a subset of points in a sample (so either or ) are unaffected by the transformation. However, this unchanged subset determines the change in the remaining points. Here, is the indices that will remain unchanged. These indices can be given to any function (typically a neural network) that returns a scaling parameter and a transform parameter . and are used to scale and shift the unmasked points.

This setup allows for coupling, or transformation of some points according to the value of other points. But we actually do not need to know the inverse of the neural network, or whatever method we use to calculate and . The Jacobian is simply a triangular matrix with the diagonal equal to 1 at the masked indices, and equal to at the unmasked indices. So the LDJ is simply the log of the product the diagonal, or where j is the number of unmasked indices (which is always 1 in a 2D example, since we leave 1 out and change the remaining).

I've modified an example provided by University of Amsterdam deep learning course for the 2D example. A simple neural network (also called a hyper-network) generates the scale and transform parameters for one of the two points based on the value of the other. The coupling layer then transforms the sample and calculates the LDJ. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# modified from https://uvadlc-notebooks.readthedocs.io/en/latest/tutorial_notebooks/JAX/tutorial2/Introduction_to_JAX.html
# and https://uvadlc-notebooks.readthedocs.io/en/latest/tutorial_notebooks/JAX/tutorial11/NF_image_modeling.html
class SimpleNet(nn.Module):
    num_hidden : int   # Number of hidden neurons
    num_outputs : int  # Number of output neurons

    def setup(self):
        self.linear1 = nn.Dense(features=self.num_hidden)
        self.linear2 = nn.Dense(features=self.num_outputs)

    def __call__(self, x):
        # Perform the calculation of the model to determine the prediction
        x = self.linear1(x)
        x = nn.tanh(x)
        x = self.linear2(x)
        return x
    
class CouplingLayer(nn.Module):
    network : nn.Module  # NN to use in the flow for predicting mu and sigma
    mask : np.ndarray  # Binary mask where 0 denotes that the element should be transformed, and 1 not.
    c_in : int  # Number of input channels
    layer_type = "Scale and Shift"
    def setup(self):
        self.scaling_factor = self.param('scaling_factor',
                                         nn.initializers.zeros,
                                         (self.c_in,))

    def __call__(self, z, ldj, rng, reverse=False):
        # Apply network to masked input
        z_in = z * self.mask
        nn_out = self.network(z_in)
        s, t = nn_out.split(2, axis=-1)
        # Stabilize scaling output
        s_fac = jnp.exp(self.scaling_factor).reshape(1, -1)
        s = nn.tanh(s / s_fac) * s_fac
        # Mask outputs (only transform the second part)
        s = s * (1 - self.mask)
        t = t * (1 - self.mask)
        # Affine transformation
        if not reverse:
            # Whether we first shift and then scale, or the other way round,
            # is a design choice, and usually does not have a big impact
            z = (z + t) * jnp.exp(s)
            ldj += s.sum(axis=[1])
        else:
            z = (z * jnp.exp(-s)) - t
            ldj -= s.sum(axis=[1])
        return z, ldj, rng

MultiLayer Network

We want to create a model with multiple layers, train it, and sample from it when we are done training. This is very simple to do with the networks we defined in flax, and the optimizers provided by optax . The sampling function could be even simpler if we didn't want to see the intermediate transformations. Notice that during sampling, we simply generate two points from a normal distribution and pass it back through the flows.

Architecture

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# multi layer network
class PointFlow(nn.Module):
    flows : Sequence[nn.Module]  
    def __call__(self, z, rng, intermediate=False,training=True):
        ldj = 0 
        rng, rng_new = jax.random.split(rng,2)
        for flow in self.flows:
            z, ldj, rng = flow(z, ldj, rng, reverse=False)
        return z, ldj, rng_new
    
    def sample(self,rng,num = 1, intermediate = False):
        ldj = 0
        rng, new_rng = jax.random.split(rng,2)
        z = jax.random.normal(rng,shape=[num,2])
        intermediate_layers = [z]
        for flow in reversed(self.flows):
            z, ldj, rng = flow(z,ldj,rng,reverse=True)
            if intermediate: # if we want to see the intermediate results
                intermediate_layers.append(z)
        return z, rng, intermediate_layers

The PointsFlow model just needs a list of flow layers, we've already defined Relu and Coupling layers. Notice that the mask variable takes on the values of [1,0] or [0,1] every other layer.

1
2
3
4
5
6
7
8
flow_layers = []
for i in range(9):
    flow_layers += [LeakyRelu()]
    flow_layers += [CouplingLayer(network = SimpleNet(num_hidden=4,num_outputs=2),mask = jnp.array([0,1]) if i%2 else jnp.array([1,0]),c_in=1)]

    
model = PointFlow(flow_layers)
params = model.init(init_rng,inp,inp_rng,intermediate=True)

Training and Sampling

Now we need to define the loss calculation and optimizer. I found that adamw worked much better than SGD and adam. The loss function is where we calculate the negative log loss, which requires an understanding of the change of variable rules which was briefly discussed earlier. Try to derive it yourself on paper to make sure you understand how it works (Lilian Wang's blog was very helpful for me in this regard)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
optimizer = optax.adamw(learning_rate=0.0001)
model_state = train_state.TrainState.create(apply_fn=model.apply,
                                            params=params,
                                            tx=optimizer)
# loss calculation
def loss_calc(state, params, rng, batch):
    rng, init_rng = jax.random.split(rng,2)
    z, ldj, rng  = state.apply_fn(params,batch,rng)
    # loss is ldj + log(probability of points in a normal distribution)
    log_pz = jax.scipy.stats.norm.logpdf(z).sum(axis=[1])
    log_px = ldj + log_pz
    nll = -log_px
    return nll.mean(), rng
    
nll, rng = loss_calc(model_state,params,rng,inp) # run it once and see the output

Finally, we define a train_step function. If you have a GPU, the jitted function runs incredibly fast. 

1
2
3
4
5
6
7
8
9
10
11
12
13
@jax.jit
def train_step(state,rng,batch):
    rng, init_rng = jax.random.split(rng,2)
    grad_fn = jax.value_and_grad(loss_calc,  # Function to calculate the loss
                             argnums=1,  # Parameters are second argument of the function
                             has_aux=True  # Function has additional outputs, here rng. Which you don't even need now that I think about it. 
                            )
    # Determine gradients for current model, parameters and batch
    (loss,rng), grads = grad_fn(state, state.params, rng, batch)
    # Perform parameter update with gradients and optimizer
    state = state.apply_gradients(grads=grads)
    # Return state and any other value we might want
    return state, rng, loss

Training is simple and very fast if you have a GPU. 

1
2
3
4
state = model_state
for i in range(50000):
    state,rng,loss = train_step(state,rng,X)
    print("iter %d patience %d loss %f"%(i,patience, loss) , end="\r")

And so is sampling: 

1
2
3
4
5
layers = ["random sample"] + [model.flows[i].layer_type for i in range(len(model.flows))][::-1] # names of generation layers (backward order of training layers)

for i,out in enumerate(mid_layers):
    sns.scatterplot(x= out[:,0], y = out[:,1],label = "out of" + layers[i])
    plt.show()
It's easier to show a gif rather than 19 scatter plots: transformation animation